How to trace the path in a Breadth-First Search?

Question

How do you trace the path of a Breadth-First Search, such that in the following example:

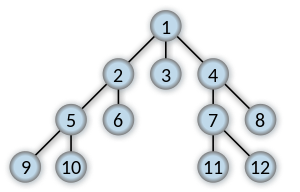
If searching for key 11, return the shortest list connecting 1 to 11.

[1, 4, 7, 11]

Answer 1

You should have look at http://en.wikipedia.org/wiki/Breadth-first_search first.

---

Below is a quick implementation, in which I used a list of list to represent the queue of paths.

# graph is in adjacent list representation
graph = {
        '1': ['2', '3', '4'],
        '2': ['5', '6'],
        '5': ['9', '10'],
        '4': ['7', '8'],
        '7': ['11', '12']
        }

def bfs(graph, start, end):
    # maintain a queue of paths
    queue = []
    # push the first path into the queue
    queue.append([start])
    while queue:
        # get the first path from the queue
        path = queue.pop(0)
        # get the last node from the path
        node = path[-1]
        # path found
        if node == end:
            return path
        # enumerate all adjacent nodes, construct a new path and push it into the queue
        for adjacent in graph.get(node, []):
            new_path = list(path)
            new_path.append(adjacent)
            queue.append(new_path)

print bfs(graph, '1', '11')

---

Another approach would be maintaining a mapping from each node to its parent, and when inspecting the adjacent node, record its parent. When the search is done, simply backtrace according the parent mapping.

graph = {
        '1': ['2', '3', '4'],
        '2': ['5', '6'],
        '5': ['9', '10'],
        '4': ['7', '8'],
        '7': ['11', '12']
        }

def backtrace(parent, start, end):
    path = [end]
    while path[-1] != start:
        path.append(parent[path[-1]])
    path.reverse()
    return path


def bfs(graph, start, end):
    parent = {}
    queue = []
    queue.append(start)
    while queue:
        node = queue.pop(0)
        if node == end:
            return backtrace(parent, start, end)
        for adjacent in graph.get(node, []):
            if node not in queue :
                parent[adjacent] = node # <<<<< record its parent 
                queue.append(adjacent)

print bfs(graph, '1', '11')

The above codes are based on the assumption that there's no cycles.