Finding an approximate local maximas with noisy data in Matlab
The matlab FAQ describes a one-line method for finding the local maximas:
index = find( diff( sign( diff([0; x(:); 0]) ) ) < 0 );
But I believe this only works if the data is more or less smooth. Suppose you have data that jumps up and down in small intervals but still has some approximate local maximas. How would you go about finding these points? You could divide the vector into n pieces and find the largest value not on the edge of each but there should be a more elegant and faster solution.
A one-line solution would be great, too.
Edit: I'm working with noisy biological images which I am attempting to divide into distinct sections.
Answer
I'm not sure what type of data you're dealing with, but here's a method I've used for processing speech data that could help you locate local maxima. It uses three functions from the Signal Processing Toolbox: HILBERT, BUTTER, and FILTFILT.
data = (...the waveform of noisy data...);
Fs = (...the sampling rate of the data...);
[b,a] = butter(5,20/(Fs/2),'low'); % Create a low-pass butterworth filter;
% adjust the values as needed.
smoothData = filtfilt(b,a,abs(hilbert(data))); % Apply a hilbert transform
% and filter the data.
You would then perform your maxima finding on smoothData. The use of HILBERT first creates a positive envelope on the data, then FILTFILT uses the filter coefficients from BUTTER to low-pass filter the data envelope.
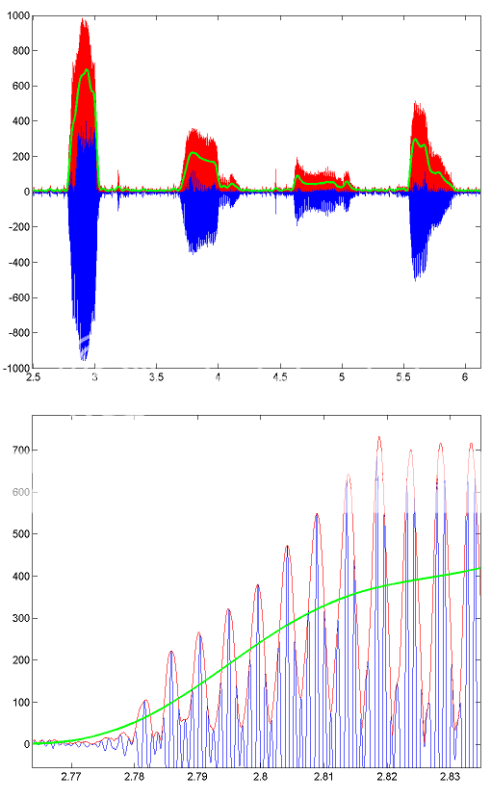
For an example of how this processing works, here are some images showing the results for a segment of recorded speech. The blue line is the original speech signal, the red line is the envelope (gotten using HILBERT), and the green line is the low-pass filtered result. The bottom figure is a zoomed in version of the first.
SOMETHING RANDOM TO TRY:
This was a random idea I had at first... you could try repeating the process by finding the maximas of the maximas:
index = find(diff(sign(diff([0; x(:); 0]))) < 0);
maxIndex = index(find(diff(sign(diff([0; x(index); 0]))) < 0));
However, depending on the signal-to-noise ratio, it would be unclear how many times this would need to be repeated to get the local maxima you are interested in. It's just a random non-filtering option to try. =)
MAXIMA FINDING:
Just in case you're curious, another one-line maxima-finding algorithm that I've seen (in addition to the one you listed) is:
index = find((x > [x(1) x(1:(end-1))]) & (x >= [x(2:end) x(end)]));