What is meant by diameter of a network?
The diagram shown on this link of the "A graph with 6 vertices and 7 edges where the vertex no 6 on the far-left is a leaf vertex or a pendant vertex." has DIAMETER 4? right or wrong?
Definitions are
The diameter of a graph is the maximum eccentricity of any vertex in the graph. That is, it is the greatest distance between any pair of vertices. To find the diameter of a graph, first find the shortest path between each pair of vertices. The greatest length of any of these paths is the diameter of the graph.
Diameter, D, of a network having N nodes is defined as the maximum shortest paths between any two nodes in the network
Diameter, D, of a network having N nodes is defined as the longest path, p, of the shortest paths between any two nodes D ¼ max (minp[pij length( p)). In this equation, pij is the length of the path between nodes i and j and length (p) is a procedure that returns the length of the path, p. For example, the diameter of a 4 4 Mesh D ¼ 6.
Answer
The Wikipedia Example
Looks like the diameter is 3 to me by definition.
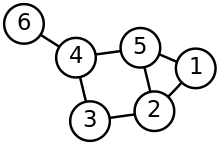
The longest shortest paths have length of 3 edges, e.g. between 6-1 and 6-2.
The Mesh Example
Here's your second definition, with some typographical correction so that it makes sense:
Diameter
Dof a network is defined as the longest path of the shortest paths between any two nodes. For example, the diameter of a 4x4 mesh D = 6
Let's take a look at the 4x4 mesh example:
A---B---C---D
| | | |
E---F---G---H
| | | |
I---J---K---L
| | | |
M---N---O---P
The longest shortest path has length of 6 edges, i.e. between A-P and M-D.
References
Mathworld - Wolfram/Graph Diameter
The length of the "longest shortest path" between any two graph vertices of a graph.
Graph and Digraph Glossary - cudenver.edu
Diameter: The diameter of a graph is the length of the longest chain you are forced to use to get from one vertex to another in that graph. You can find the diameter of a graph by finding the distance between every pair of vertices and taking the maximum of those distances.
See also
- Computing Distances and Diameter
- Has examples on weighted graphs