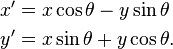Proper Trigonometry For Rotating A Point Around The Origin
Do either of the below approaches use the correct mathematics for rotating a point? If so, which one is correct?
POINT rotate_point(float cx,float cy,float angle,POINT p)
{
float s = sin(angle);
float c = cos(angle);
// translate point back to origin:
p.x -= cx;
p.y -= cy;
// Which One Is Correct:
// This?
float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;
// Or This?
float xnew = p.x * c + p.y * s;
float ynew = -p.x * s + p.y * c;
// translate point back:
p.x = xnew + cx;
p.y = ynew + cy;
}
Answer
To carry out a rotation using matrices the point (x, y) to be rotated is written as a vector, then multiplied by a matrix calculated from the angle, θ, like so:

where (x′, y′) are the co-ordinates of the point after rotation, and the formulae for x′ and y′ can be seen to be