Initial guess for Newton Raphson
How can I determine the initial guess of the equation Ax+Bsin(x)=C in terms of A,B and C ?
I am trying to solve it using Newton Raphson. A,B and C will be given during runtime.
Is there any other method more efficient than Newton Raphson for this purpose ?
Answer
The optimal initial guess is the root itself, so finding an "optimal" guess isn't really valid.
Any guess will give you a valid solution eventually as long as f'(x0) != 0 for any step, which only occurs at the zeroes of cos(x), which are k*pi + pi/2 for any integer k.
I would try x0 = C * pi, just to see if it works.
Your biggest problem, however, would be the periodic nature of your function. Newton's method will be slow (if it even works) for your function as sin(x) will shift x0 back and forth over and over.
Precaution:
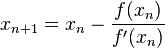
In Newton's method, do you notice how f'(xn) is in the denominator? f'(x) approaches 0 infinitely many times. If your f'(x) = 0.0001 (or anywhere close to zero, which has a chance of happening), your xn+1 gets thrown really far away from xn.
Worse yet, this can happen over and over due to f'(x) being a periodic function, which means that Newton's method might never even converge for an arbitrary x0.